By Nalin. This was joint work with Jonathan Wang, Yi Sun, Vincent Huang -- the circom-pairing team.
In this blog post, we present circuits for recursive groth16 SNARK verification in Circom, building off of previous work by the circom-pairing team. More interestingly, we introduce properties uniquely enabled by recursive zkSNARKs, and share some of our own projects that utilise these properties.
If you'd prefer a video summarisation of this blog post, check out my talk from the Applied ZK Workshop at the Science of Blockchain Conference!
Recursive zkSNARKs unlock a powerful new dimension for zkSNARKs as a cryptographic tool. But first off, what does recursion even mean in the context of a zkSNARK?
Recursing inside of a SNARK means verifying a SNARK proof inside of another SNARK proof--generating SNARK proofs of statements like "I know a zkSNARK proof which a SNARK verification algorithm returns 'true' on." Recursion allows a zkSNARK prover to squeeze more knowledge into their proofs while maintaining the succinctness properties of a SNARK: verification of a recursive zkSNARK is not significantly slower than ordinary verification.
Why would you want to make recursive SNARK proofs? Abstractly, recursive SNARKs unlock two novel application-level properties: compression and composability.
Recursive zkSNARKs allow provers to put “more knowledge” into proofs, while ensuring that these proofs can still be verified in constant or polylogarithmic time by a verifier. Therefore, using recursive ZK SNARKs as a “rollup” for information is a natural and very mechanical use case. Recursive SNARKs enable compression of information, which is a way to abuse the properties of succinctness of ZK proofs.
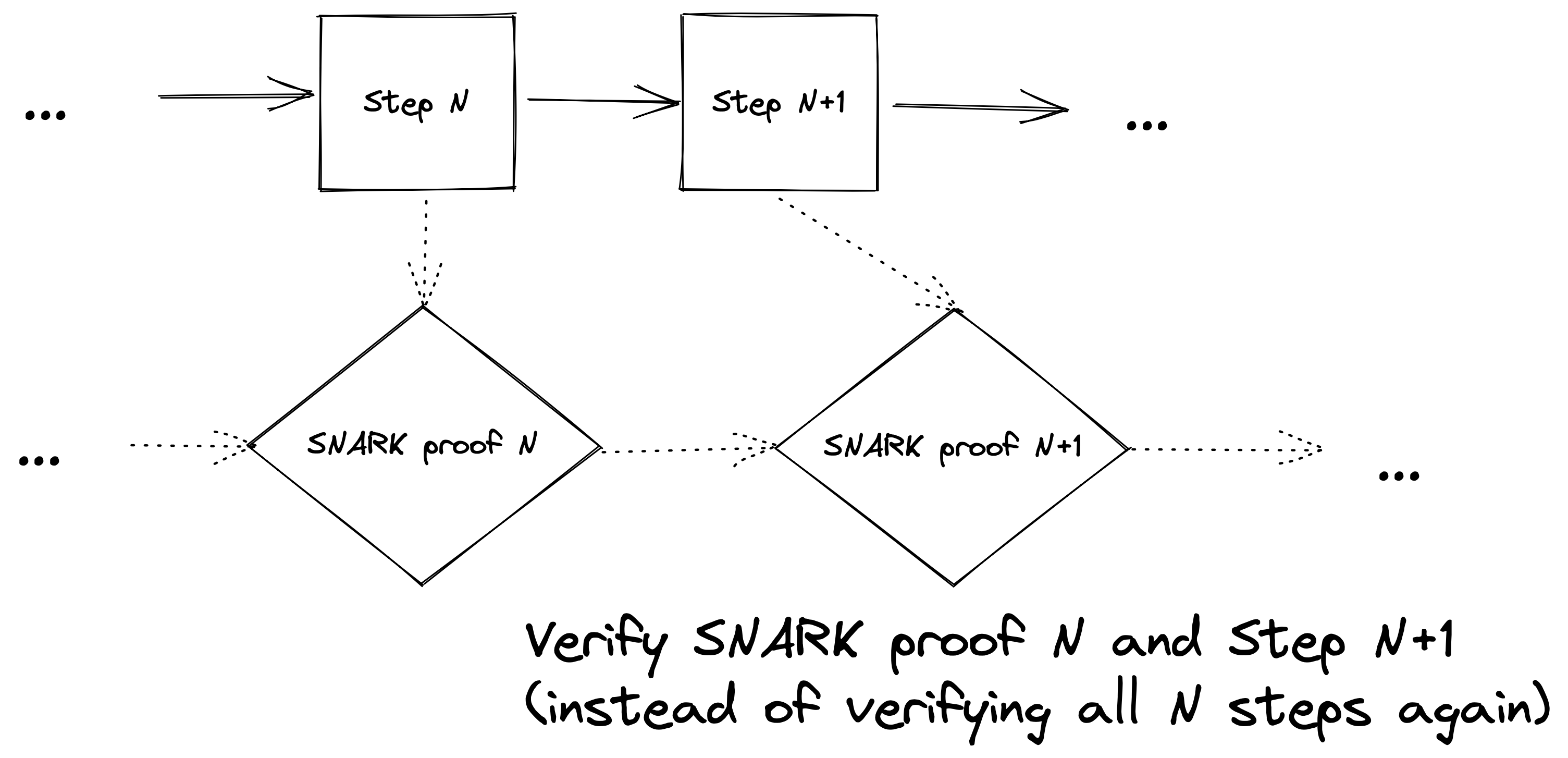
These rollup compressions all tend to share a common pattern. Suppose you have a sequence of items you want to prove, and suppose you've already generated a SNARK proof of the first N items in the list. To extend this proof to N + 1 items, you can simply generate another proof that proves two things: the validity of your previous proof of the first N items, and the validity of the N+1th item. The alternative, non-recursive approach would have been to verify all N+1 items from scratch.
In the naive model, proving cost (proving time, constraint count, trusted setup size etc.) scales linearly with the number of items being proven. On the other hand, the recursive approach bounds the marginal proving cost to the cost of one recursive proof verification plus the cost of checking one item inside the SNARK. This difference is also particularly notable for cases where these items are from streaming data. This general pattern is typically referred to as Incrementally Verifiable Computation.

Of course, rollups for monetary transactions (and EVMs) are hot in blockchain land these days, but there are other applications where compression is useful. Here are some of them:
Notably, the compression property also allows us to circumvent practical circuit size limits. Most proving system require memory on the order of the size of the circuit, so the computation we can do in ZK circuits often gets bounded by the size of hardware RAM we can acquire2. By using recursive zkSNARKs for compression, we can instead create a smaller circuit which, with the overhead of recursion, can allow us to roll up more computation than the largest (non-recursive) circuits independently can.
Outside of just rollup-like applications, there’s another neat application of compression: more expressive circuits! To elaborate, for one, you can do true conditional statements using recursive checks for a fixed cost: you can use a recursive SNARK to write a constant cost selector! Without recursion, the only way to write a dynamic selector (an expression that allows you to select the value of the Nth element of a list, where N as well as the list are dynamic inputs) is to write a loop through the list and compare every individual element, incurring O(length of list) constraints. With recursion, however, you can prove the execution of such a selector inside a SNARK, so you can roll it up inside a different circuit for the cost of SNARK verification -- which is constant This is quite interesting, since with a good enough DSL compressions could make SNARK circuit writing feel much closer to writing Turing complete machines with more freedom over looping, conditionals etc. rather than the finite state machines they feel like right now. In fact, this is also how the recently announced Lurk Language uses recursive ZK SNARKs.
Succinctness properties of vanilla zkSNARKs scale up into the compression property for recursive zkSNARKs, so it is worth asking the same question for the zero-knowledge properties of vanilla zkSNARKs: How does ZK "scale up" for recursive zkSNARKs? We've been calling this scaled up property composability:
Typically, we think of zkSNARKs in the context of "A prover shows knowledge of a fact to a verifer, without revealing the fact". There is a somewhat implicit assumption that the prover themselves are well aware of the fact itself.
Recursive zkSNARKs, however, change this. A prover can now show knowledge of a fact to a verifier, without knowing the fact themselves.
What does this mean? Using Recursive zkSNARKs, a chain of proofs could be created, where at each step the proof is passed along to a new participant, who adds on some claims of knowledge of their own. At the end, you would be able to create a combined proof of knowledge such that no individual participant in this chain has the entirety of the knowledge that antecedes this proof. Perhaps, this might also be reminiscent of how Trusted Setup ceremonies work.
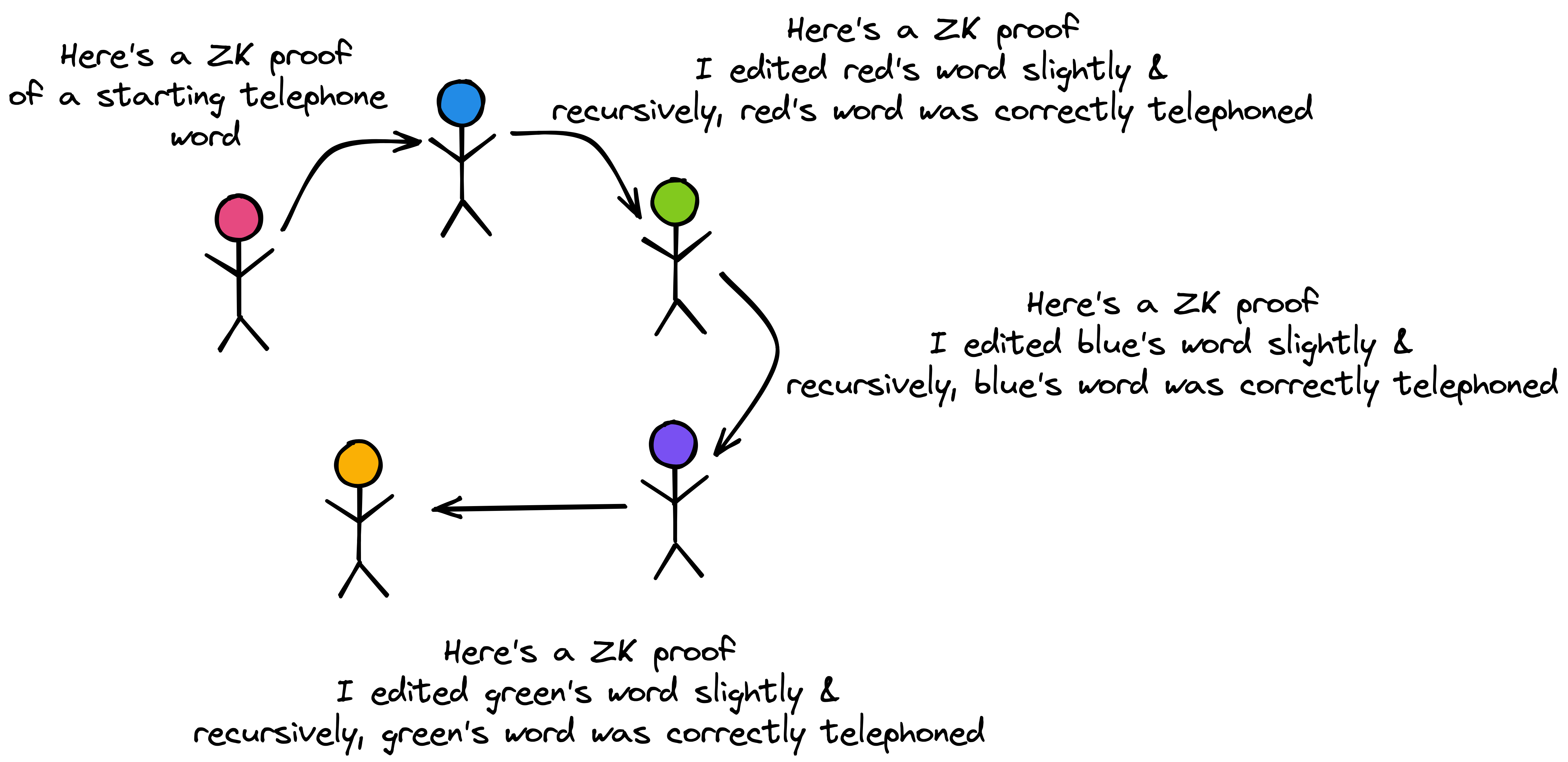
I first thought of this property in the context of the game of Telephone/Chinese whispers. No one learns the series of changes that led to the current word, but they are assured of its correctness by a zkSNARK.
Where can we use this property? A natural fit seems to be partial information games: We could use Recursive zkSNARKs to instrument party games like Mafia and Telephone between adversarial players.
But this also goes beyond games. Recently, we released ETHdos, which demonstrates a clever use case for this new property: hiding social graphs while making trustless claims about proximity!
In ETHdos, I can prove I am degree 4 from Vitalik by showing that I am friends with someone who is degree 3 (and they repeat this themselves recursively). I can show there exists a valid path of 4 people between me and Vitalik, without knowing anything about the first 3 nodes in the path.
This is something new entirely. Not only are ZK proofs hiding information from external verifiers, but also from the chain of provers themselves. This suggests that applications of Recursive zkSNARKs must be richer than that of vanilla zkSNARKs.
Another interesting idea of an application composability somewhat uniquely enables is trust-less, private liquidity channels (or even proper state channels by throwing in a zkVM), revealing none of the intermediate transactions to anyone except each other. Additionally, validity proofs would allow for minimal wait periods.4
Now that we've described some examples of composability, you'll notice a couple common threads all these constructions seem to share. Let's solidify these:
Firstly, it seems there's always multiple parties involved in these constructions: Almost certainly, it somehow doesn't make sense to use this property of recursive zkSNARKs for an individual prover. There must necessarily be some collaborative component to the proof generation process -- otherwise there is no secondary prover to hide the first proof's inputs from.
Secondly, all of these constructions use knowledge of signatures as the transitive hidden witness5 -- this isn't a coincidence, signatures are the easiest way to instantiate existential unforgeability: Only the owner of the keypairs can create these signatures, so they're great collaborative surface to build on top of. So, perhaps, one way to find interesting applications of this property is to ask: what are different things people can tuck in these collaborative cryptography boxes?
There are some close parallels between this property and how academia generally models Proof Carrying Data in how they extend Incrementally Verifiable Computation to graph structures, but largely, this seems to be one of the most overlooked properties of recursive ZK SNARKs by practitioners. We're hoping these notes will help change this and bring about cooler applications for recursive zkSNARKs.
Beyond these application-level properties unlocked by recursion, another very useful unlock on the technical side worth mentioning is the ability to mix-and-match different proof systems and arithmetisations (and with that, utilise the best features of each one). For instance, STARKs, with their AIR arithmetisation, are particularly well suited for state machine execution proofs, but are unfortunately expensive to verify. With recursion, you could generate a STARK proof for a state machine's execution, but then verify the STARK proof in a PLONK SNARK, obtaining a cheap to verify SNARK proof as output. Notably, this is the architecture that Polgon Hermez's zkEVM (using an EVM as the state machine) uses.
Now that we've established why recursive zkSNARKs are interesting, let's zoom in to how we implemented recursive zkSNARKs in groth16, and how you can use our work to build your own circuits:
While there has been a ton of research on building ZK SNARKs efficient at recursion on the proving systems layer (eg Halo 2, Nova), most of this work has not yet permeated into software libraries developers can play with. However, groth16, one of the very first general purpose zkSNARK schemes (albeit one that's very vanilla and has been superseded by other constructions on almost all dimensions) has a thriving developer tooling ecosystem around it in the form of Circom, snarkjs, rapidsnark, and other related libraries.
So, while groth16 is not particularly well suited for recursion from a theoretical perspective, enabling recursion for the groth16 paradigm is a surefire way to enable explorations with recursive SNARKs on the application layer today!
Typically, there are two methods for implementing fully-recursive SNARKs: the more popular one is using cycles of pairing-friendly elliptic curves, where efficient recursion is enabled by finding two pairing friendly curves such that the order of one equals the field size of the other, and vice versa. This cycle allows the recursive zkSNARK protocol to alternate field operations between these two, only requiring a small amount of wrong-field math/conversions. A second way is to brute-force your way through and simply implement elliptic curve operations for a single pairing friendly curve in your proving system itself (by doing a bunch of ugly, "wrong-field" bigint math).
We take the latter approach. With circom-pairing team’s work, we already had all the necesary primitives (pairing checks and EC operations) required to build out a groth16 proof verifier in Circom. So, earlier this summer, Jonathan Wang and I ported the pairing circuits to the BN254 curve and then put together a groth16 verifier in Circom - open sourced here!

The Optimisoor of a groth16 verification inside SNARKs
Using a number of neat optimisation tricks (lightly detailed in the screenshot above for those more familiar with the verification scheme), we were able to get the groth16 verification circuit down to ~20M constraints! Unfortunately, 20M constraints is still quite a lot and far from the reach of client-side proving on laptops/desktops6. Ultimately, we are able to generate recursive SNARK proofs in about 250 seconds on a beefy server (32-core 3.1GHz, 256G RAM). This can be further optimised to about 180 seconds with some devops tricks detailed in ETHdos's blog post. While this is certainly limiting in its current form, we think unlocking the possibility of an entirely new class of applications is nonetheless very exciting!
While as an application developer you can ignore most of the details of this verification, it is important to be aware of two facts about this verification:
For the first limitation, we introduce a trick to compress many public inputs into one: All the inputs that are meant to be public are instead passed as private inputs into the circuit, and the only public input exposed is a hash of these private inputs. In addition to its usual checks, the circuit additionally verifies that the hash of the private (or more aptly, semi-public inputs) matches the passed public input hash. Under the Fiat-Shamir model, this is secure as you would essentially need to find another "useful" preimage for the publically passed hash. This trick has use cases beyond just recursion. In other verification environments, you can use this trick to reduce verification compute cost (for instance, saving gas costs for an on-chain groth16 proof verifier).
Regarding the second limitation, you'll notice that perhaps the applications most suitable for recursive groth16 SNARKs are ones that recurse into themselves, i.e. proofs verified in the circuit are proofs of the same circuit itself. This would mean we only require one trusted setup. We'll share our mental model for thinking about making applications with self-recursive SNARKs in this context:
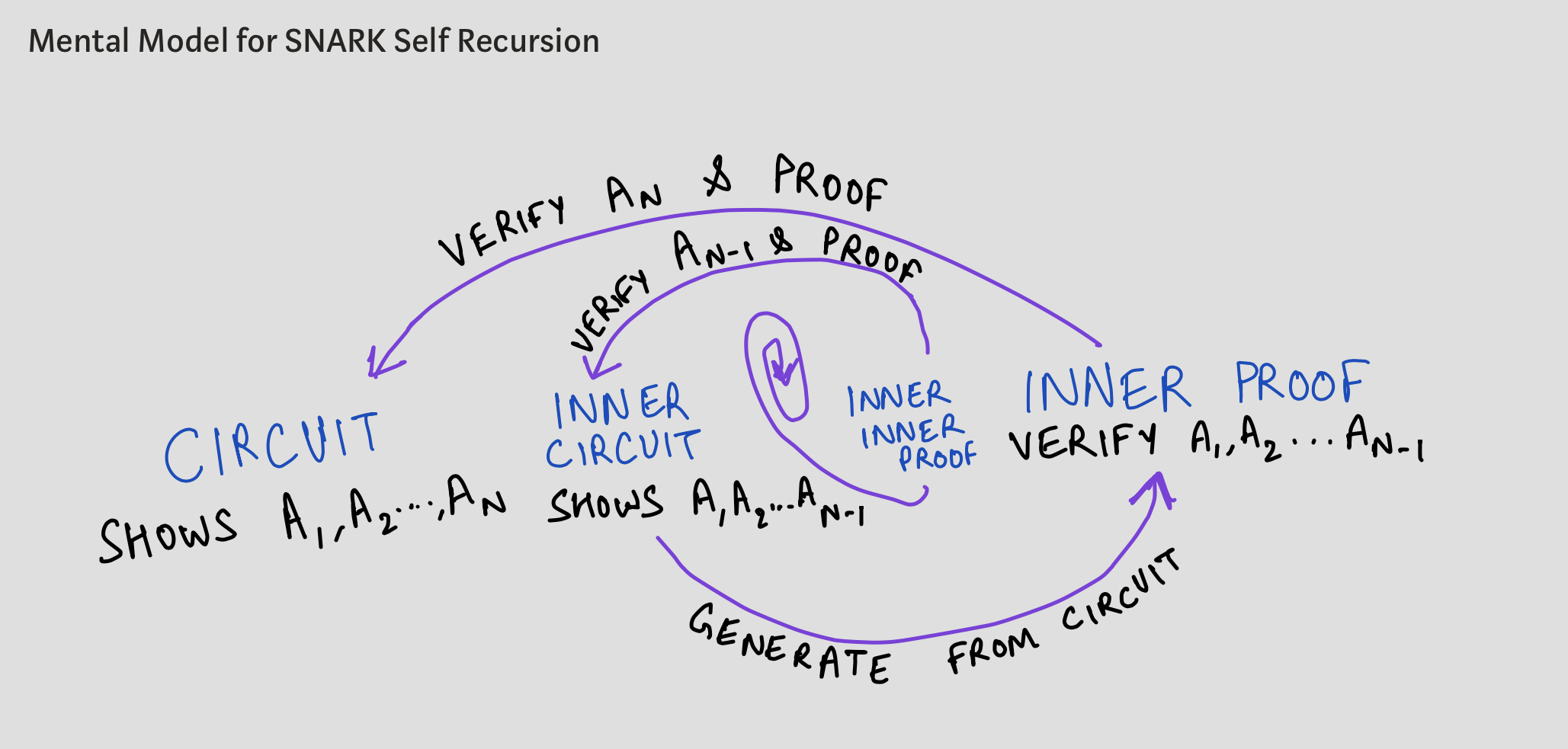
How to think about self-recursive SNARKs
At each step, you have a circuit that proves the validity of computation A_i, A_{i+1} \dotsAi,Ai+1… (with perhaps ii as a public input to the SNARK), and within the iith such proof, you verify another proof showing validity of computation A_{i+1}, A_{i+2} \dotsAi+1,Ai+2… alongside step A_iAi's validity. At each recursion, your SNARK circuit would remain the same. In the case of Isokratia, for example, each of the A_iAis are ECDSA signature verifications.
In the next post, we'll release and detail the construction of Isokratia and expand on how to use these two tricks and mental models in practice. In the meantime, check out our previous blog post on ETHdos.
Thanks to Jonathan Wang, Yi Sun, Vivek Bhupatiraju, Sampriti Panda, Adhyyan Sekhsaria, Ying Tong, Barry Whitehat, Lakshman Sankar, Amir Bolous and others in the 0xPARC community for helping consolidate these ideas and reviewing drafts of this post.
Typically, blockchain light clients have the ability to provide proofs of values of individual state values on-chain. ZK-SNARKs allow compressing many such proofs, along with aggregation functions like SQL, to generate succinct proofs of historical data and trends of state values on-chain.↩
Or in the case of groth16 and other trusted setup based SNARKs, the maximum size of the circuit gets bounded first by a different practical limit, the size of the largest trusted setups we have available (that are currently on the order of 228 constraints).↩
2^{28}
In case of Circom based recursive SNARKs, this constant cost is very high making it useless in practice, but the general strategy is interesting to keep in mind.↩
Here’s a full description of the liquidity channel protocol using this: two parties escrow into a contract and do a bunch of transactions off chain between each other, revealing none of the intermediate transactions to anyone except each other. At all times, they maintain a rollup zk proof that has 3 public inputs: both the parties balances and the number of transactions between them (this will be useful later for indexing). Each time I want to make a proof, I generate a signature attesting to a transaction at a particular state, and roll it up into a new zk proof and give it to my counterparty. My counterparty does the exact same thing back. At no point are signatures revealed to each other; only the balance sheet is revealed. At any point, if one of them decides to settle, they can on chain and show the rolled-up zk proof to the contract, revealing only final balances. To complete the construction, you would need a escalation game style mechanism in case any single party tries to go to chain and censor some suffix of transactions. In such a case, the counterparty would use the "index" public parameter to be able to show a “larger” (by number of transactions) zk proof and guarantee correct settlement. Two open questions on this protocol: Can you layer this protocol on top of an anonymity pool to hide transactors? Can you build Lightning Network style channels with multi-hop payments using this?↩
This can be slightly generalised to be problems in NP, which is really what Digital Signature Algorithms (and ECC) unlock for us on-demand. Notably, factorisation is another such problem in NP which might be interesting to think more deeply about.↩
Based on 0xPARC's previous work pushing in-browser proving to its limits with heyanon and stealthdrop, 20M constraints is over by a factor of ~10x or so for what's possible in-browser today.↩
在这篇博文中,我们介绍了 Circom 中递归 groth16 SNARK 验证的电路,该电路基于 circom-pairing 团队之前的工作。更有趣的是,我们介绍了递归 zkSNARKs 唯一启用的属性,并分享了我们自己的一些利用这些属性的项目。
如果您更喜欢这篇博文的视频摘要,请查看我在区块链科学会议应用 ZK 研讨会上的演讲!
递归 zkSNARKs 为 zkSNARKs 作为一种加密工具开启了一个强大的新维度。但首先,递归在 zkSNARK 的上下文中意味着什么?
在 SNARK 中递归意味着在另一个 SNARK 证明中验证 SNARK 证明——生成诸如“我知道一个 SNARK 验证算法返回‘真’的 zkSNARK 证明”之类的语句的 SNARK 证明。递归允许 zkSNARK 证明者将更多知识压缩到他们的证明中,同时保持 SNARK 的简洁性:递归 zkSNARK 的验证并不比普通验证慢很多。
为什么要进行递归 SNARK 证明?抽象地说,递归 SNARK 解锁了两个新的应用级属性:压缩和可组合性。
递归 zkSNARK 允许证明者将“更多知识”放入证明中,同时确保这些证明仍然可以由验证者在恒定或多对数时间内进行验证。因此,使用递归 ZK SNARK 作为信息的“汇总”是一个自然且非常机械的用例。递归 SNARK 可以压缩信息,这是滥用 ZK 证明简洁性的一种方式。
这些汇总压缩都倾向于共享一个共同的模式。假设您有一系列要证明的项目,并且假设您已经生成了列表中前 N 个项目的 SNARK 证明。要将这个证明扩展到 N + 1 个项目,您可以简单地生成另一个证明来证明两件事:您之前对前 N 个项目的证明的有效性,以及第 N+1 个项目的有效性。另一种非递归方法是从头开始验证所有 N+1 个项目。
在朴素模型中,证明成本(证明时间、约束计数、可信设置大小等)与被证明的项目数量呈线性关系。另一方面,递归方法将边际证明成本限制为一个递归证明验证的成本加上检查 SNARK 中的一个项目的成本。对于这些项目来自流数据的情况,这种差异也特别显着。这种通用模式通常称为增量可验证计算。

当然,如今,货币交易(和 EVM)的汇总在区块链领域很热门,但还有其他应用可以使用压缩。这里是其中的一些:
Isokratia:将链下投票汇总成一个可验证的链上 SNARK 证明,滥用简洁性来实现〜免费、信任最小化的治理。请继续关注本周即将发布的 Isokratia!👀
区块链轻客户端:滥用压缩以在一个 ZK 证明中证明整个区块链的有效性,并最大限度地减少对全节点的信任假设。这就是Celo 的 Plumo 轻客户端的
工作方式。
去信任的链上索引器和聚合器:如果你可以将 SQL VM 放在 ZK SNARK 中,那么就像轻客户端 SNARK 一样,你可以启用链上数据的去信任查询和聚合,并构建一个更去中心化和更低信任的版本的**图表1**
。
VDF 证明者:VDF(可验证延迟函数)是计算缓慢但需要易于验证的函数。您可以使用递归 SNARK 来压缩 VDF 函数的有效性证明,在 SNARK 递归内运行几轮 VDF 函数。
值得注意的是,压缩特性还使我们能够规避实际电路尺寸的限制。大多数证明系统需要电路大小数量级的内存,因此我们可以在 ZK 电路中进行的计算通常受到我们可以获得的硬件 RAM 大小的限制2。通过使用递归 zkSNARK 进行压缩,我们可以创建一个更小的电路,利用递归的开销,可以让我们比最大的(非递归)电路独立地汇总更多的计算。
除了类似汇总的应用程序之外,还有另一个简洁的压缩应用程序:更具表现力的电路!详细地说,首先,您可以使用递归检查对固定成本进行真正的条件语句:您可以使用递归 SNARK 来编写恒定成本选择器!在没有递归的情况下,编写动态选择器(允许您选择列表的第 N 个元素的值的表达式,其中 N 和列表都是动态输入)的唯一方法是编写一个循环遍历列表并进行比较每个单独的元素,都会产生 O(列表长度)约束。然而,通过递归,您可以证明这样一个选择器在 SNARK 中的执行,因此您可以在不同的电路中将其卷起,以获得 SNARK 验证的成本——这是恒定的!3这很有趣,因为使用足够好的 DSL 压缩可以使 SNARK 电路编写感觉更接近于编写图灵完备的机器,在循环、条件等方面有更多的自由,而不是他们现在感觉的有限状态机。事实上,这也是最近公布的Lurk Language使用递归 ZK SNARK 的方式。
vanilla zkSNARKs 的简洁性属性扩展到递归zkSNARKs 的压缩属性,因此值得对 vanilla zkSNARKs 的零知识属性提出相同的问题:ZK 如何“扩展”递归zkSNARKs?我们一直称其为按比例放大的属性可组合性:
通常,我们在“证明者向验证者展示事实知识,而不透露事实”的上下文中考虑 zkSNARKs。有一个隐含的假设,即证明者自己很清楚事实本身。
然而,递归 zkSNARKs 改变了这一点。证明者现在可以向验证者展示对事实的了解,而他们自己并不知道事实。
这是什么意思?使用递归 zkSNARKs,可以创建一个证明链,在每个步骤中,证明都会传递给一个新参与者,新参与者会添加一些他们自己的*知识声明。*最后,您将能够创建一个组合的知识证明,这样该链中的任何个体参与者都不会拥有该证明之前的全部知识。或许,这也可能让人想起Trusted Setup 仪式的运作方式。

我第一次想到这个属性是在电话/中文窃窃私语游戏的背景下。没有人知道导致当前单词的一系列变化,但他们可以通过 zkSNARK 确保其正确性。
我们可以在哪里使用这个属性?部分信息游戏似乎很适合:我们可以使用 Recursive zkSNARKs 来检测诸如Mafia和Telephone等敌对玩家之间的派对游戏。
但这也超越了游戏。最近,我们发布了ETHdos,它展示了这个新属性的一个巧妙用例:隐藏社交图,同时对接近度做出不信任的声明!
在 ETHdos 中,我可以证明我是 Vitalik 的 4 级,通过证明我是 3 级的人的朋友(并且他们自己递归地重复这一点)。我可以证明在我和 Vitalik 之间存在 4 人的有效路径,而对路径中的前 3 个节点一无所知。
这完全是新事物。ZK 证明不仅对外部验证者隐藏信息,而且对证明者链本身也隐藏信息。这表明递归 zkSNARKs 的应用必须比普通 zkSNARKs更丰富。
应用程序可组合性的另一个有趣想法是无需信任的私有流动性通道(甚至是通过引入 zkVM 的适当状态通道),除了彼此之外,不会向任何人透露任何中间交易。此外,有效性证明将允许最短的等待时间。4
既然我们已经描述了一些可组合性的示例,您会注意到所有这些结构似乎共有的几个共同点。让我们巩固这些:
首先,似乎这些构造总是涉及多方:几乎可以肯定的是,将递归 zkSNARKs 的这种属性用于单个证明者是没有意义的。证明生成过程必须有一些协作组件- 否则没有辅助证明者可以隐藏第一个证明的输入。
其次,所有这些结构都使用签名知识作为传递隐藏见证5 - 这不是巧合,签名是实例化存在不可伪造性的最简单方法:只有密钥对的所有者才能创建这些签名,所以它们是可以在其上构建的出色协作表面。所以,也许,找到这个属性的有趣应用的一种方法是问:人们可以在这些协作密码盒中塞进什么不同的东西?
该属性与学术界在如何将增量可验证计算扩展到图结构方面通常如何建模证明携带数据之间存在一些密切的相似之处,但在很大程度上,这似乎是从业者最容易忽视的递归 ZK SNARK 属性之一。我们希望这些笔记将有助于改变这一点,并为递归 zkSNARKs 带来更酷的应用程序。
除了这些通过递归解锁的应用级属性之外,另一个值得一提的技术方面非常有用的解锁是混合和匹配不同证明系统和算术的能力(并利用每个人的最佳特性)。例如,具有 AIR 算法的 STARK特别适合状态机执行证明,但不幸的是验证成本很高。通过递归,您可以为状态机的执行生成 STARK 证明,然后在 PLONK SNARK 中验证 STARK 证明,从而获得廉价的验证 SNARK 证明作为输出。值得注意的是,这是Polgon Hermez 的 zkEVM(使用 EVM 作为状态机)使用的架构。
既然我们已经确定了为什么递归 zkSNARK 很有趣,让我们深入了解我们如何在 groth16 中实现递归 zkSNARK,以及如何使用我们的工作来构建自己的电路:
虽然已经有大量关于在证明系统层(例如Halo 2、Nova)上构建高效递归的 ZK SNARK 的研究,但其中大部分工作尚未渗透到开发人员可以使用的软件库中。然而,groth16 是最早的通用 zkSNARK 方案之一(尽管它非常普通,并且在几乎所有维度上都被其他结构所取代)围绕它有一个蓬勃发展的开发者工具生态系统,形式为 Circom、snarkjs、rapidsnark 和其他相关库。
因此,虽然从理论的角度来看 groth16 并不是特别适合递归,但启用 groth16 范式的递归是当今在应用层上使用递归 SNARK 进行探索的可靠方法!
通常,有两种实现完全递归 SNARK 的方法:更流行的一种是使用循环配对友好椭圆曲线,其中通过找到两条配对友好曲线来实现有效递归,使得一个阶数等于其他,反之亦然。这个循环允许递归 zkSNARK 协议在这两者之间交替进行字段操作,只需要少量的错误字段数学/转换。第二种方法是强行通过并简单地在证明系统本身中为单个配对友好曲线实现椭圆曲线操作(通过执行一堆丑陋的“错误字段”bigint 数学)。
我们采取后一种方法。通过 circom-pairing 团队的工作,我们已经拥有了在 Circom 中构建 groth16 proof 验证器所需的所有必要原语(配对检查和 EC 操作)。所以,今年夏天早些时候,我和 Jonathan Wang 将配对电路移植到了 BN254 曲线,然后在 Circom 中组装了一个 groth16 验证器——在此处开源!
